A Guide to Moore and Mealy Machines
Finite State Machines (FSMs) are computational models used to represent and control the behavior of systems through states and transitions. They’re widely used in areas such as digital circuit design, compiler design, communication protocols, and software modeling. This post describes two fundamental types of FSMs: the Moore machine and the Mealy machine
Finite State Machines
An FSM consists of:
- States: Defined configurations representing various possible situations the system can be in.
- Inputs: Events or signals that trigger transitions between states.
- Outputs: Results or actions associated with states or transitions.
- Transitions: Rules determining state changes based on inputs.
- Initial State: The starting point of the machine.
FSMs can be represented using state tables and/or state diagrams. State tables consist of Current State, Next State, Input and Output columns and state transition rows. State diagrams consist of circles representing states, arrows denoting transitions, and labeled inputs/outputs.
Moore and Mealy Machines
Moore Machines
In Moore machines, the current output is determined solely by the current state of the machine. The input affects transitions between states, but not the output directly.
Formal Definition
A Moore machine is a 6-tuple:
: Finite set of states.
: Initial state,
: Finite set of input symbols (alphabet).
: Finite set of output symbols (alphabet).
: State transition function,
.
: Output function,
.
Properties
- The output depends only on the current state.
- They often require more states compared to Mealy machines.
State Diagram Representation
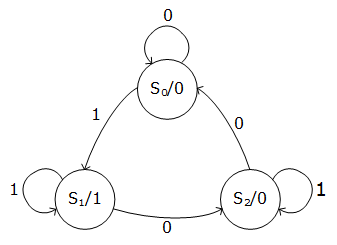
- The input is represented with each transition.
- The output is represented with each state.
Mealy Machines
In Mealy machines, the output depends on both the current state and the current input. Hence, outputs are associated with transitions rather than states.
Formal Definition
A Mealy machine is a 6-tuple:
.
Properties
- The output depends on both current state and input.
- They often require fewer states compared to Moore machines.
State Diagram Representation
coming soon
Key Differences
| Feature | Moore Machine | Mealy Machine |
|---|---|---|
| Output depends on | Current state | Current state and input |
| Output association | With states | With transitions |
| Number of states | Typically more | Typically fewer |
| Speed of response | Slower (output after state) | Faster (output during transition) |
| Complexity of design | Simpler output logic | Slightly more complex output logic |
Practical Applications
- Moore Machines:
- Traffic light control systems
- Vending machines with outputs dependent on internal state (e.g., current amount of money inserted)
- Control logic circuits
- Digital locks and security systems
- Elevator control systems
- Game states
- Industrial controllers
- Mealy Machines:
- Real-time communication protocols
- Data transmission and encoding systems
- Signal edge detection in digital circuits
- Interactive User Interfaces
- Real-time control systems
- Error detection and correction
Summary
- Moore Machines have state-based outputs, simpler to understand but may require more states.
- Mealy Machines have transition-based outputs, allowing fewer states and faster reactions, but slightly more complex logic.
Choosing between Moore and Mealy machines depends on the specific application requirements, complexity constraints, and speed of output responses required.